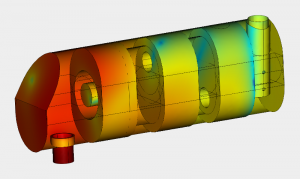
Ausgangspunkt für die Anwendung der FEM ist, wie bei allen anderen numerischen Berechnungsverfahren, die Diskretisierung der Struktur in eine Vielzahl von interagierenden Teilgebieten, die so genannten finiten Elemente (z. B. Dreiecke, Tetraeder).

Auf der Basis von gegebenen Randbedingungen (z. B. Quell- und Materialparameter) werden die den physikalischen Vorgang repräsentierenden Differentialgleichungen in ein lineares Gleichungssystem zur Berechnung der unbekannten Knotenpunktparameter umgewandelt und gelöst.