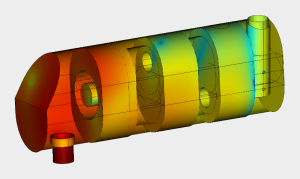
As in case of any other numerical calculation method, the starting point for the application of the FEM method is the discretization of the structure into a great number of interacting partial areas, the so-called finite elements (e.g. triangles, tetrahedra).

On the basis of given constraints (e.g. source and material parameters), the differential equations describing the physical process are transformed into a linear equation system for the computation of the unknown nodal point parameters and solved.